You are here
Historic Volatility (HVOL)
The Historic Volatility indicator is used mainly as an option evaluation tool. It does not give trading signals like those given with other technical indicators. It gives the trader an idea of how volatile the market has been for a previous period of time.
Changing the period of time the study observes allows the trader to finetune options prices. If a market has been extremely volatile for the past 3 months, for example, near term options should be more expensive. If the market has been calm for an extended period of time, longer term options should be reasonable. In futures, we use it for observation. It tells us if prices are calming down or becoming more erratic.
The key to using historic volatility is determining the correct period of time for each market. The market you are looking at may show a history of volatility years ago, but has been relatively calm the last few months. Getting an idea of the markets behavior recently may be of no use to the trader that is looking at distant options.
For the futures trader, this tool is useful as a guide for order placement. Changing market volatility may indicate that it is time to move stops closer or farther away. If the trader is profitable with the trend and volatility is changing, it might be a time to move stops closer to protect profits. If a trader is trading against the trend, he might want to move stops further away to avoid getting bumped out prematurely.
Options traders could use this study to help them purchase profitable options. The basic idea is to buy options when volatility is decreasing to take advantage of a change in that volatility. Any rise in volatility will translate to an increase in option values. Look at options strategies that take advantage of low volatility, such as straddles or ratio spreads. When volatility is high, selling options would be better because any decrease in volatility will translate to a loss of option value. Option strategies that take advantage of a decrease in volatility are strangles and regular short option positions.
Obviously, historic volatility is only one component of option pricing. Any changes in the underlying futures market could negate the changes in option prices due to volatility. For example, if you were to buy a low volatility Put option and prices go higher, that option will lose value but not as quickly as a higher volatility option.
For the futures trader, the basic concept is to expect market changes during periods of increased volatility. George Soros, the trading legend, said "Short term volatility is greatest at a turn around and diminishes as a trend becomes established."
This indicator is commonly viewed as very mean regressive. What this term means is that the historic volatility indicator tends to return to the opposite end of the spectrum and therefore return to an average. If volatility is great it will eventually cool off and return to that place. If volatility is low it will not stay quiet forever. What this means to traders is that a market that is erratic will sooner or later calm down and a market that is quiet will eventually get loud again.
Calculation
The calculation for the historical volatility is rather involved. The number of periods per year vary depending on the type of price chart used for the study. The following table lists the number of periods for each type of chart:
| Chart Type | Trading Periods Per Year |
|---|---|
| Perpetual | 252 |
| Daily | 252 |
| Weekly | 52 |
| Monthly | 12 |
| Variable | Based on chart period (see below) |
| Tick | Not available for this study |
When using variable charts, you must first calculate the number of trading periods per year. To do this, you must determine the trading time of the selected commodity. The formula is as follows:
TP = (Tt / Pn) x 252
TP: The total number of trading periods per year.
Tt: The total trading time in a day.
Pn: The length of the period.
252: The number of weekdays per year.
Example: The S&P 500 trades from 8:30 a.m. to 3:15 p.m. That is a total trading time of 6 hours and 45 minutes. On a variable chart using 5 minute bars, the number of periods for the day is 81:
6 hours x 60 minutes = 360 minutes + 45 minutes
Total minutes of trading = 405 minutes
405 / 5 minute bars = 81 trading periods per day
Now that you have calculated the trading periods per day, you now must calculate the number of periods for the year. Since historical volatility considers every weekday of the year when calculating total periods for the year, the multiplier is 252:
TP = (405/5) x 252
TP = 81 x 252 TP = 20,412
Note: This formula applies only to historical volatility on a variable chart. It does not apply to other chart types.
Now that you have the total number of periods per year, continue with the calculation of the historical volatility, by calculating the natural logarithm of the price change for each price in the specified time span of n periods:
LOGSi = LOG(Pi / Pi-1)
LOG: The natural logarithm function.
Pi: The current price.
Pi-1: The previous price.
Now that you have the natural logarithms of the price changes, calculate the total natural logarithms for the time span you are reviewing:
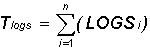
Tlogs: The total of the natural logarithm price ratio for the time span.
S: Indicates to sum all n natural logarithms.
LOGSi: The natural logarithm of the price change for period i.
N: The number of periods for the specified time span.
The next step is to calculate the average of the logs by dividing the total natural logarithm by the number of periods:
ALOGS = Tlogs / n
ALOGS: The average of the natural logarithms.
Tlogs: The total of the natural logarithm for the time span.
N: The number of periods for the specified time span.
The last calculation is to sum the squares of the difference between the individual natural logarithms for each period and the average natural logarithm:
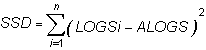
SSD: The sum of the squared differences.
S: Indicates to total the squares of all n differences.
LOGSi: The natural logarithm of the price change for period i.
ALOGS: The average of the natural logarithms.
Now that the elements of the final formula are complete, the following formula calculates the historical volatility for a given period over a specified time span:
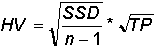
SSD: The sum of the squared differences.
n: The number of periods for the specified time span.
TP: The total number of trading periods for the year.
Due to the complexity of the formula, it is preferable to use a scientific calculator when attempting to manually calculate the historical volatility of a futures instrument.
Example of Historical Velocity in the Indicator Window

Preferences
Right-click on the HVOL button in your Indicator toolbar and select HVOL Settings. The Preferences Tab will open in the Control Panel and the HVOL preferences will be displayed. (Once you click on the chart, the Preference tab will go back to chart settings.)
Restore Settings: TNT Default will change your settings back to the original software settings. My Default will change current settings to your personalized default settings. Apply To All Charts will apply your selected settings on all open charts. Save As My Default will save your current personal settings.

HVOL Period: The number of bars, or period, used to calculate the study. Default is 20. You may use any number greater than 1 for the close.
HVOL: Choose the color, line style, and line thickness of your line. Click to Show Relative Scaling if you want the 100% location to be changed to the highest point value in the indicator.
View up to four Thresholds at values and colors of your choice.
